数独（Sudoku）是一种数学逻辑游戏。对于 9 阶的标准数独，其搜索状态树节点数量少，简单的回溯法能很快解算出结果，因此不作为并行算法的讨论对象。16 阶与 25 阶数独，其状态树的深度与广度都要比 9 阶数独大，简单的回溯法已经无法快速地完成计算，需要利用并行方法进行加速。

算法简介

数独（Sudoku）是一种数学逻辑游戏。如图 1 所示，标准数独由 $9\times 9$ 个格子组成，玩家需要根据格子提供的数字推理出其他格子（cell）的数字。一般情况下设计者会提供最少 17 个数字（known numbers）使得解答谜题只有一个答案。数独要求每一行（row）、每一列（colume）以及每一宫（block）的数字都不缺少也不重复。数独还存在阶数更高的变体，如 $16\times 16$ 和 $25\times 25$ 的高阶数独。

​数独的程序解法一般可用回溯法（Back Tracking）来实现，算法包括以下几步：

• 筛选候选数（cadidate）
• 回溯法暴力求解数独

筛选候选数的目的在于减少每一个未知格里的候选数，从而减少搜索状态树的节点数量，提高搜索速度。有的算法还会采用逻辑解法进一步减少候选数的数量。回溯法则是一种基于深度优先遍历的搜索算法，通常利用递归实现。

算法分析

对于 9 阶的标准数独，其搜索状态树节点数量少，简单的回溯法能很快解算出结果，因此不作为并行算法的讨论对象。16 阶与 25 阶数独，其状态树的深度与广度都要比 9 阶数独大，简单的回溯法已经无法快速地完成计算，需要利用并行方法进行加速。

针对一个简单的 25 阶数独，算法的两部分的用时比较如表 1 所示。可以看到，算法最耗时的部分是回溯法求解数独环节，基本决定了总耗时，我们需要对这一部分算法进行基于 MPI 的并行化改进。

算法步骤	用时（秒）
筛选候选数（剪枝）	0.002
回溯法求解数独	448.535

针对数独求解的相应串行伪代码如下所示：

python
# search for result using backtracking with recursion
def backTracking(sudoku: Sudoku)->bool:
    if sudoku.isFinished():
        return True
    cell = sudoku.findNextUnfinishCell()
    for num in cell.cadidate:
        if sudoku.isValidNum(cell, num)
            sudoku.do(cell, num)
            if backTracking(sudoku):
                return True
            sudoku.undo(cell)
	return False

并行设计

本实验的数独回溯法并行求解基于 MPI 多进程实现，且采用主从模式进行并行，设计过程依照 PCAM 方法。

划分

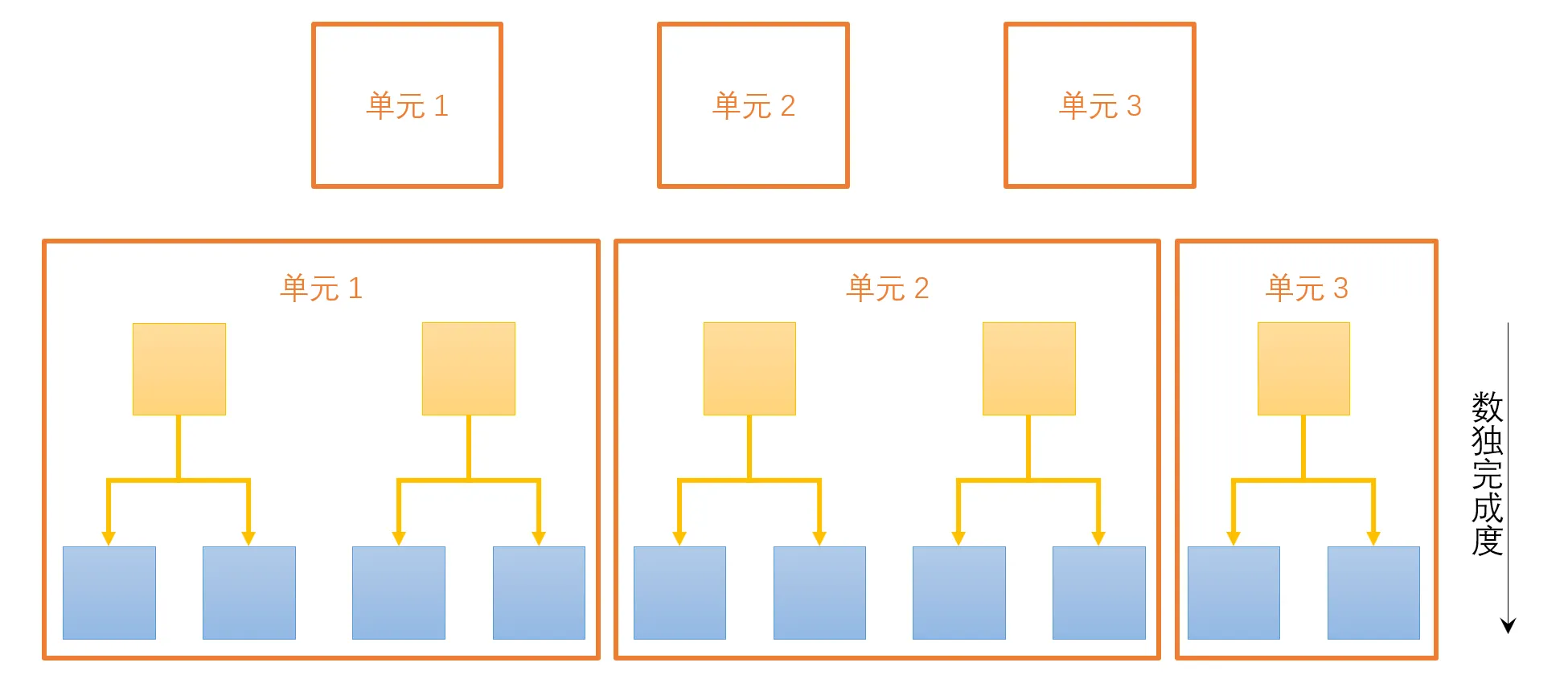
如图 2 所示，回溯法求解数独本质上是一种搜索空间的深度优先遍历，每一个节点都可以看作是一个数据，需要验证其是否矛盾（直到出现完成的节点）。同时由于回溯法的递归特性，数独回溯算法可以拆分成完成度更高的若干个数独（后称“子数独”）进行并行回溯（如图 3 所示）。因此对于数独回溯算法，可以利用域分解进行划分。

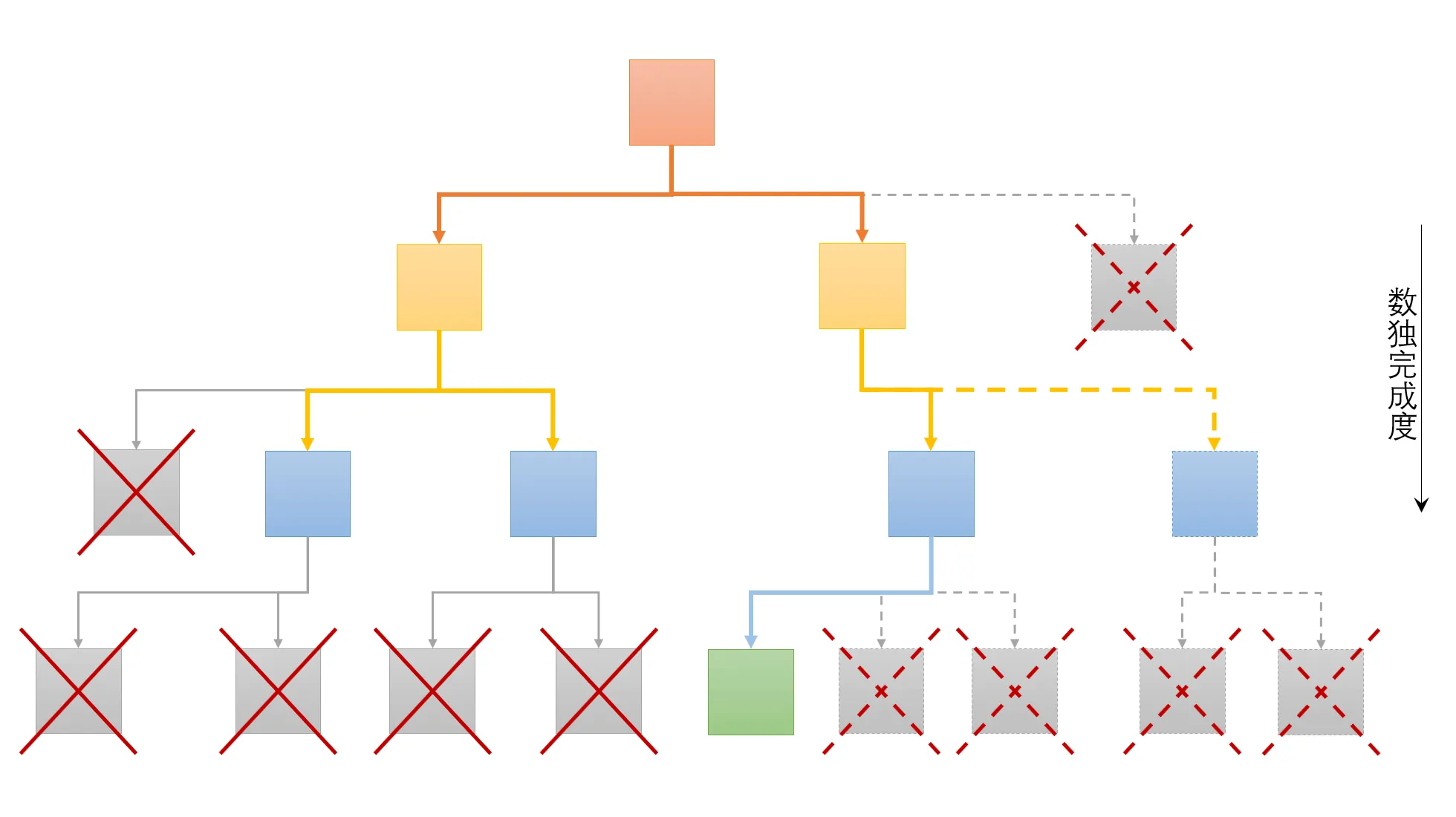
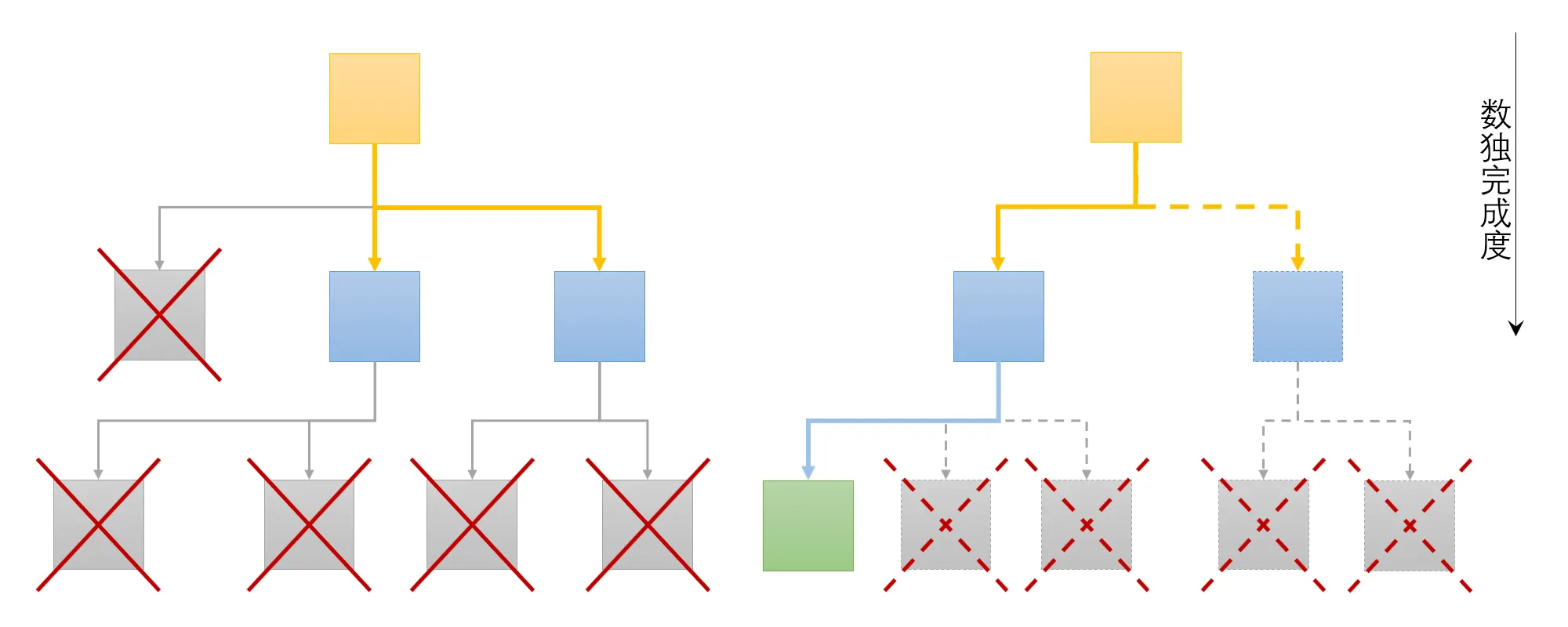
因为搜索空间是一个树结构，每多一个未填格，树结构就会增加一层，搜索数量会指数级增加。所以应当保证每个并行单元的子数独完成度一致，否则并行单元之间的任务尺寸可能会不同，影响并行效率。利用广度优先遍历，可以保证拆分得到的子数独完成度相同，位于树结构的同一层。

然而，利用广度优先遍历拆分得到的子数独数量（任务数量）不一定与并行单元数相同，任务粒度太粗后分配任务的数量依然会存在差距，需要把任务的粒度划分得更细，以弥补并行单元之间任务分配数量的差距，具体讨论放在组合映射部分。而任务分配涉及的通信问题放在下一节讨论。

通信

每个并行单元的子数独都是独立的数独，不存在流依赖、反向依赖或是输出依赖，所以计算时并行单元间不存在通信的问题，很容易并行化。但是在进行任务分配时，则存在并行单元之间的通信。采用主从模式并行时，主节点承担着任务划分和分配的功能，从节点承担主要的计算任务，从节点的计算依赖主节点划分的任务数据。

通信采用点对点阻塞通信，其中涉及的通信包括：

• 主节点向从节点发布任务
• 从节点完成任务向主节点报告是否解决数独
• 主节点通知从节点结束工作

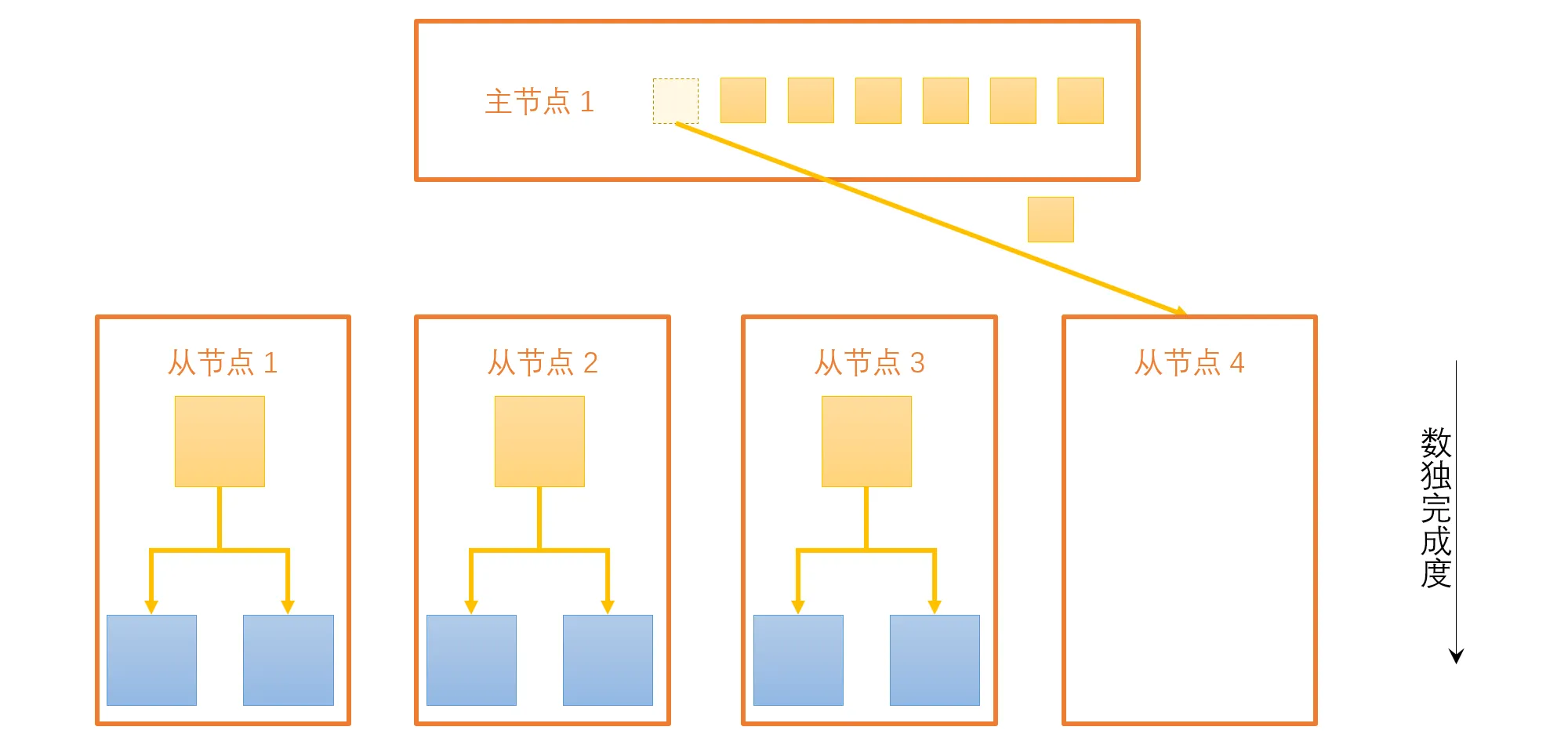
一般来说，主节点存储着一个任务队列，在从节点完成当前任务后，主节点将一直向从节点发布新的任务，直到任务队列清空（如图 4）。这一过程中，会涉及多次主节点与从节点之的通信。

组合与映射

在划分一节中，提到了任务数量与并行单元数量不相同的问题。由于我们采用的是主从并行模式，任务队列里的任务（理论上）会均匀分发给每个子节点，如果任务数除以子节点数存在余数，那么就会有一些子节点多分得一个任务。任务粒度过粗，会使得多出的这一个任务的处理时间要明显超过其他子节点，出现子节点闲置时间过长的现象。细化任务粒度，增加任务数量，能够减少这部分多出的时间，有助于主节点任务队列实现负载均衡。

而因为主节点任务队列的存在，每个子节点完成任务后都会从任务队列获取新的任务，组合与映射是一个动态的过程，与程序的运行情况有关。

并行算法

并行的算法与串行算法差异不大，主要是任务分配需要特别处理，其伪代码如下：

python
def backTracking(sudoku: Sudoku)->bool:
    // backTracking is similar to the serial one
	pass

// master process
def master()->NoReturn:
    // other initial work
    ...
    // use BSF to find sudokus 
    // that have same unknown cells
    sudokuQue = sudoku.splitSubSudoku() 
    while unfinished:
        if slaveFinishTask(slave):
            if success():
                break
            if sudokuQue.length()>0:
                assignTask(sudokuQue.popFront(),slave)
    sendTerminateMessage(slaves)
    // other work
    ...
    
// slave processes
def slave()->NoReturn:
    // other initial work
    ...
    // always fetch new task until get terminate message
    while not terminate():
    	// if no more sudoku
    	// slave will be blocked until terminate 
        receiveSubSudoku(sudoku)
        if backTracking(sudodu):
            sendSuccessMessage(master)
        else
            sendFailMessage(master)
        
    // other work
    ...

需要注意的是，实际代码实现中的阻塞点对点通信函数不是伪代码这样调用的，伪代码屏蔽了 MPI 通信中的具体操作。具体代码实现可参见我的 github 仓库

实验分析

实验准备

实验的测试数据使用了此项目中的测试数据。但选题、实现与实验均未参考该项目。如图 6 所示，测试数据是一个 25 阶的数独，由于控制测试用时的原因，减少了未填格的数量，盘面有 15 个宫基本填好了数字。

并行化基于 MPI 实现，使用 Microsoft MPI 在 Windows 平台上开发运行并行应用程序，编程语言为 C++。程序采用主从模式进行并行，由一个主进程负责拆分和分发任务，其他子进程负责计算。

实验结果

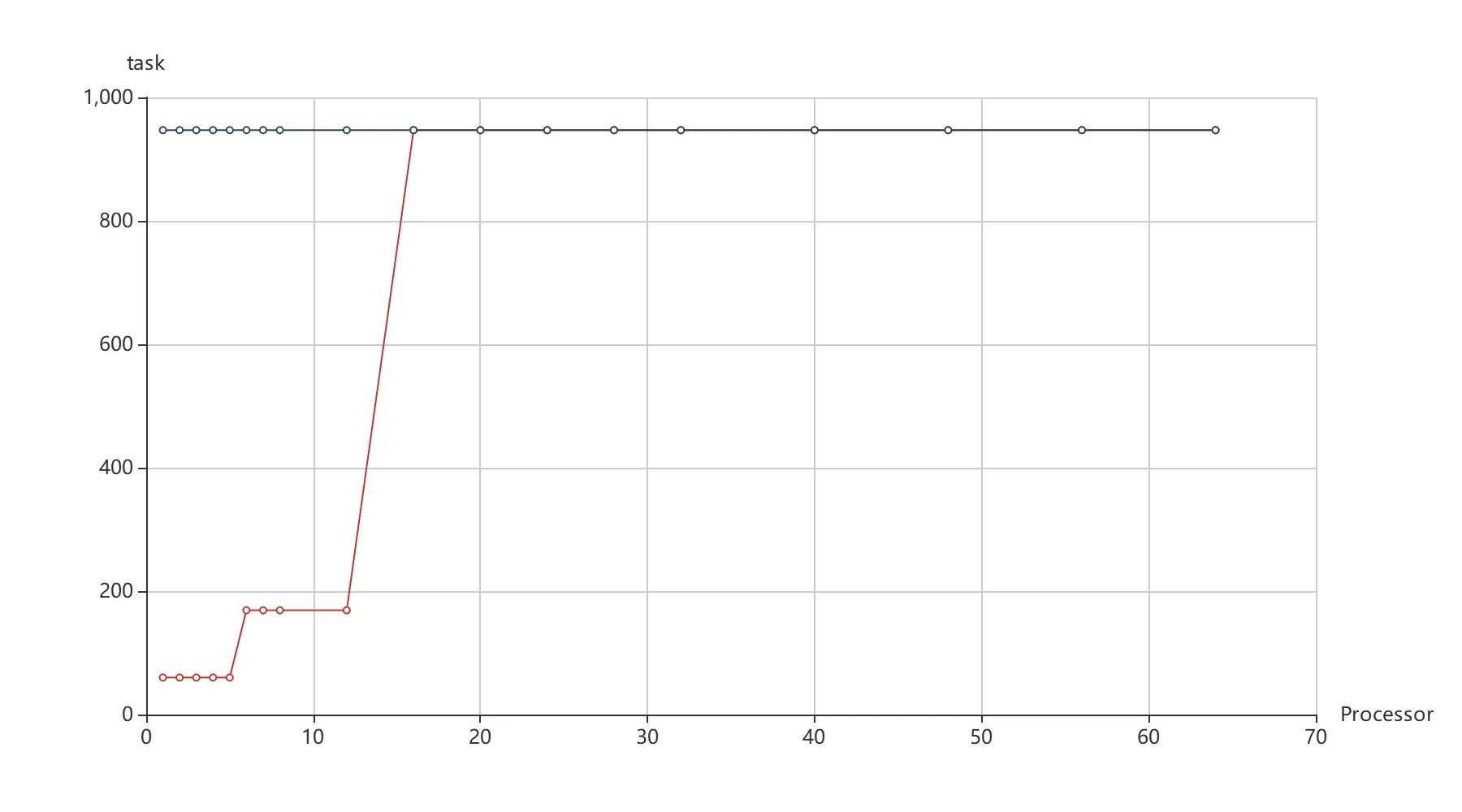
图 7 红色折线展示了实验进程数与划分任务数的关系，（蓝色折线为另一对比实验，将在下文讨论）。代码中设置的任务数量应为进程数量的 10 倍以上，但是由于数独划分的要求（如前所述，需要保证子数独完成度一致），其数值是受到限制的，所以会呈现出图 7 中红色折线阶跃的现象。

并行算法加速比与进程数的关系如图 8 所示。在 1-20 个进程并行时，加速比趋近于线性增长。之后由于并行开销累积，计算资源限制，加速比增长趋于平缓。

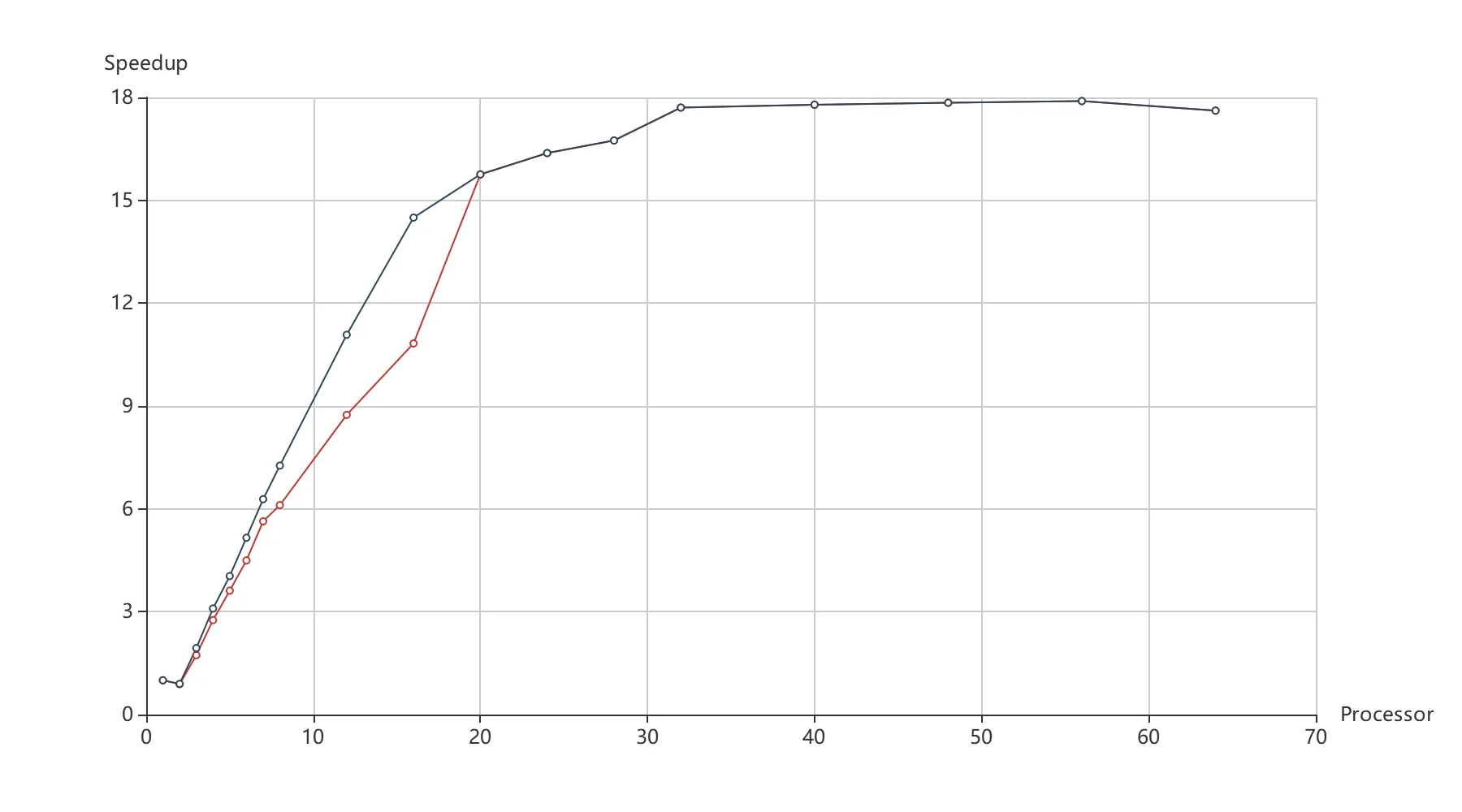
在这里，虽然该折线与 Amdahl 定律给出的折线相近，但个人认为并不是 Amdahl 定律造成的。

其一，算法的串行开销并不大，主进程任务拆分必须在所有子进程运算之前，可以认为是串行开销，这部分用时仅在 0.1 秒以内（2000 个任务时，实际上会更短）。并行化之前，筛选候选数只需要执行一次，并行化之后由于通信时需要将数独类序列化的原因，每个任务都需要重新执行一次，但每次筛选候选数用时仅 0.002 秒，按 1 个进程 50 个任务，用时也不超过 0.1 秒。相比于实验中耗时 25 秒（并行前 450 秒）的结果，基本可以忽略。

其二，由于实验的多进程运行在同一台主机上，其计算资源有限。测试中，当进程数在 28 时（恰好对应图 8 进入平台的折点），电脑的 CPU 利用率就已经到达 100% 了，所以增加更多的进程对算法的加速影响不大了，这一点应该才是折线趋于平缓的原因。

并行算法的并行效率如图 9 所示。由于算法基于主从模式，主进程是不参与主要计算的，所以在进程数设置为 2 时，加速比依然为 1，因而并行效率在这里有一个陡降。后随着并行进程数的增加，这一影响逐渐消失。进程数为 8-16 时，红色折线也出现了一次下降。结合图 7 可以发现可能是由于任务数量的问题（恰好对应任务数为 169），划分不够细导致并行效率下降。当将任务数全固定为 947 时，并行效率如蓝色折线所示，折线 8-16 进程的下降情况消失，可见任务划分粒度对并行效率也有很大影响。

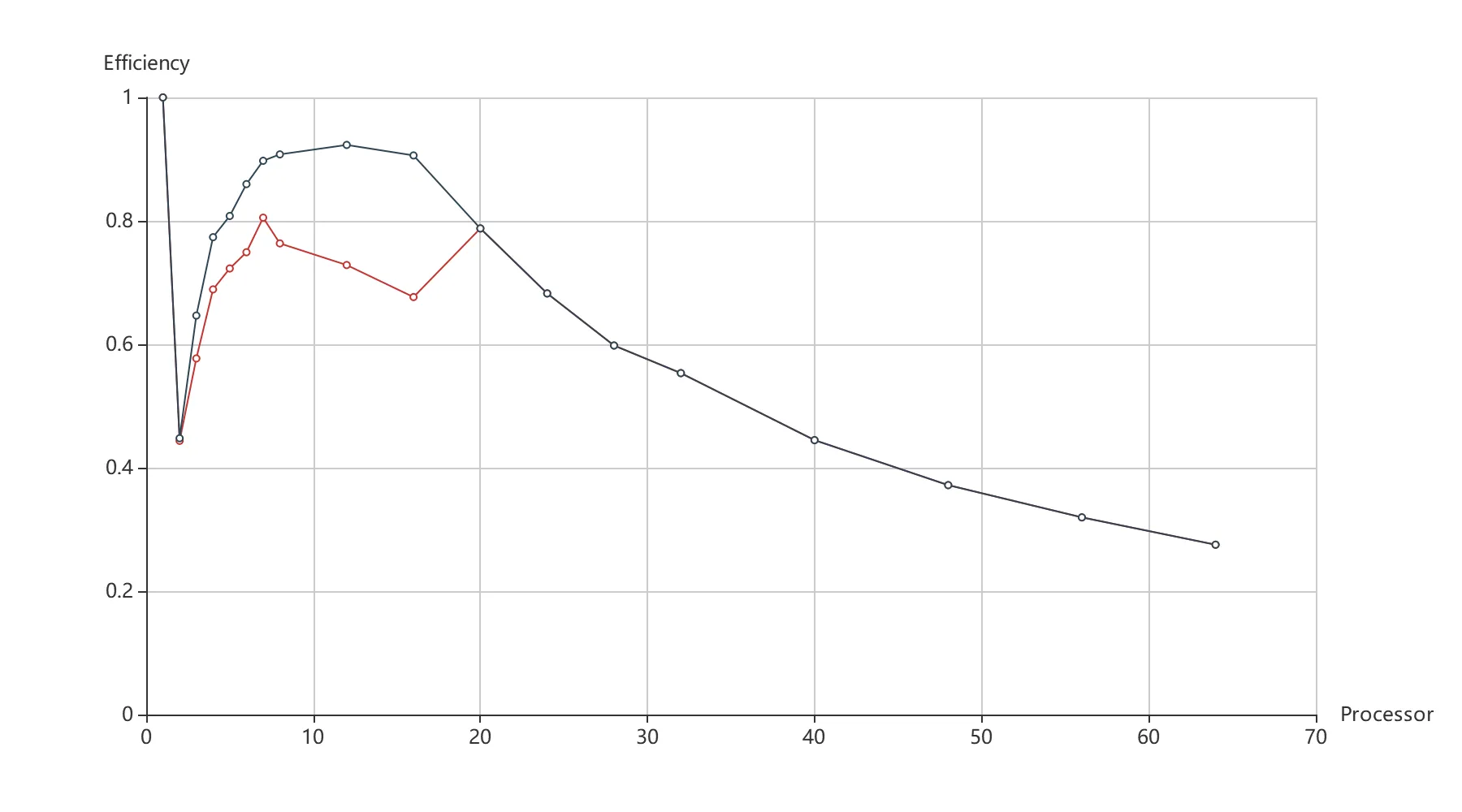
实际上，当进程数为 20-64，任务数提升到 2099 甚至 7563 时，加速效果基本没有提升（如表 2）。因此可以认为，20-64 并行进程的任务划分已足够细。

指定任务数	160	2000	4000
实际任务数	947	2099	7563
20 进程并行实际用时	28.469	28.453	29.574
64 进程并行实际用时	25.463	25.404	25.765

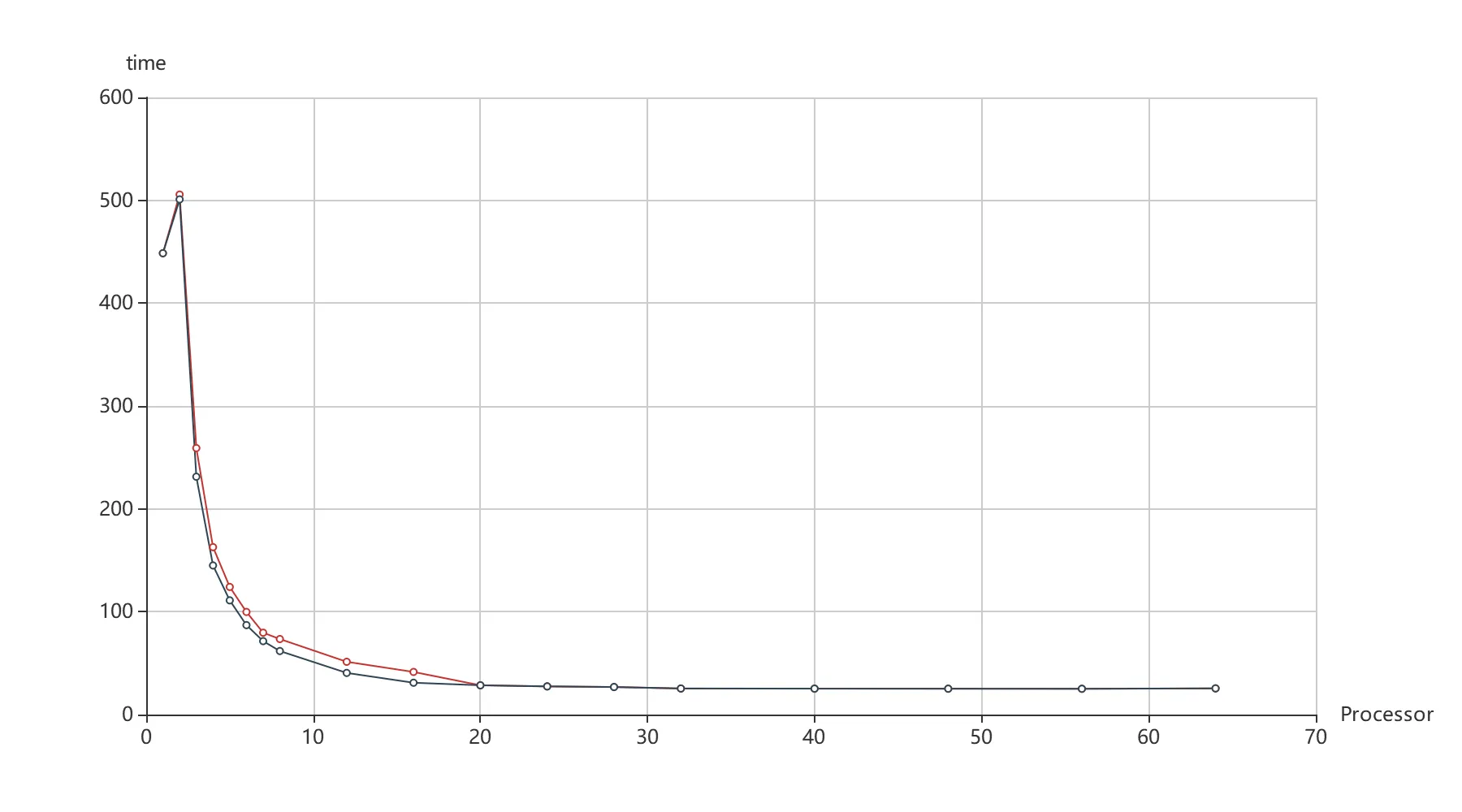
两次实验用时对比如图 10 所示。总体来说，并行实验的加速效果显著，实验取得了成功。

个人心得

并行算法的编程思维不同于串行算法，通过这次的实验我切切实实地感受到了并行算法编程的难度，也体会到并行算法在高性能计算上的威力。

并行算法需要考虑的东西有很多，光是控制任务尺度一致就花费了我很长的时间，因为任务数与进程数没办法完美平均地进行组合映射，最后才想到了利用任务列表动态进行分配的办法。然而任务队列也没办法解决所有的问题，当我使用串行 50 秒计算完成的数据测试时，加速比与并行效率很快就饱和了，而且计算很低效。计算过程中出现了其他进程跑完了所有任务，而一个进程一直还在计算的情况（即该任务计算量很大）。编程过程中甚至考虑了利用双向队列实现任务窃取算法避免这种情况（太复杂没能实现）。后来换用串行 450 秒计算完成的数据测试时，呈现效果才比较好。可能是由于之前使用的数据状态树较浅，不平稳的情况更严重，而整个并行任务是从树的根结点开始分配的，这就导致分配任务的计算量还是存在差距过大的问题。所以理论与实际情况还是有一定的差别，只有实际实验过才明白其中存在的问题。

在选题过程中我参考了不同的资料，想到了不少的有趣的问题，在选择时也是纠结了很长时间。最后因为出于选题新颖度、呈现效果、PCAM 分析出的题目复杂度和个人编程能力的考量排除了这些选项，但不列出又深感遗憾，遂呈现在这里。

其他候选题目：

• 八皇后问题
  • 对回溯法进行数据并行
  • 不够新颖，而且是书上介绍的题目
  • 基于此问题联想到数独求解问题
• 矩阵乘法的 Cannon 并行算法
  • 是一个针对存储的优化计算，可能并不能进行串并行的比较分析
• 矩阵 LU 分解的并行算法
  • 不够新颖
  • 略复杂
• 离散数学中的稳定匹配问题
  • 存在并行可能，直觉上是适合并行的算法，但并行化算法的有效性并不确定
  • 存在通信同步问题，需要解决读写问题
• 计算机视觉中的切图算法 Seam Carving

  • 边缘检测算子计算能量图

    • 涉及卷积的并行，并行化没有难度

  • 动态规划计算最小的切分路径

    • 可数据并行，但是计算依赖其他单元上一步的计算结果，涉及到通信同步问题
• 计算几何中平面最近点对的分治算法
  • 和 $k$-d 树以及分治构建三角网的算法比较像，可能不够新颖

参考文献

• 陈国良. 并行计算系列丛书: 并行算法实践[M]. 高等教育出版社

• GENE H. GOLUB‚ CHARLES F. VAN LOAN. Matrix computations[M]. Fourth edition. Baltimore: The Johns Hopkins University Press‚ 2013.

• Discrete Mathematics and Probability Theory Course Note: Note 4

• Seam Carving — Interactive Computational Thinking — MIT

• 平面最近点对 - OI Wiki